Die Bundesregierung, die Tagesschau und die Exponentialrechnung
Äh…naja.
Die Faktenchecker von der Tagesschau klären uns auf:
Geisterspiele, abgesagte Messen und Konzerte sollen die Ausbreitung des #Coronavirus verzögern – und eine Überlastung des Gesundheitssystems verhindern. #Corona pic.twitter.com/pQ9DFWKDzC
— tagesschau (@tagesschau) March 12, 2020
Screenshot daraus:
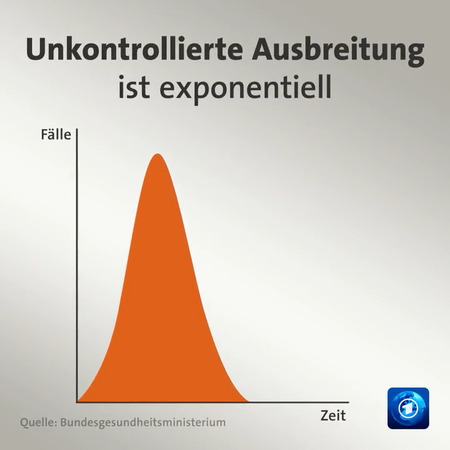
„Quelle: Bundesgesundheitsministerium”
Sieht so exponentielles Wachstum aus? Ist das exponentielles Wachstum?
Es ist eine Gauß-Glocke, eine Normalverteilung. Nun kommt in der Dichtefunktion der Normalverteilung (was eben die berühme Gauß-Glocke ist) zwar tatsächlich die Exponentialfunktion vor, allerdings mit negativem Vorzeichen im Exponenten und zudem quadriertem Parameter. Die ist deshalb nicht das, was man so im allgemeinen als „exponentiell” bezeichnet.
Ob die Dichte der Neuinfektionen nach einer Normalverteilung erfolgt, halte ich auf den ersten Blick zumindest so ungefähr für naheliegend, aber nicht zwingend, denn die Ansteckung ist kein völlig zufällig laufender Prozess. Exponentiell erscheint er einem, weil „jeder Infizierte steckt x weitere an” zwar eine Exponentialfunktion beschreibt, die aber nur gilt, solange jeder Infizierte auf dieselbe Zahl frischer Nicht-infizierter trifft und mit der gleichen Wahrscheinlichkeit neue auslöst. Das aber nimmt recht schnell wieder ab, weil man irgendwann ja nicht mehr nur ständig auf neue trifft, und die Leute schon infiziert sind, und man ja auch nicht ständig Fremde trifft. Wer heute seine Familie, Freunde oder Arbeitskollegen traf, wird sie auch morgen treffen, und nicht jeden Tag gegen frische auswechseln.
Im Prinzip hat das große Ähnlichkeit mit einer Atombombe, bei denen zerfallende Atome weitere anstoßen, aber auch nur, solange genug Vorrat da ist. Und es hat Ähnlichkeit mit den „Schneeball”-Betrugssystemen, der progressiven Kundenwerbung, bei denen auch jeder, der einzahlt, danach x neue werben muss, und das zusammenfällt, wenn es irgendwann nicht mehr genug neue Leute gibt.
Insofern müsste der Anteil derer, die bereits Kontakt mit dem Virus hatten, der Verteilungsfunktion entsprechen.
Es mag also schon sein, dass die Dichte der Neuinfektionen, also die Nachrichten-typische Zahl der täglichen Neuinfizierten, so ungefähr normalverteilt ist (exakt kann sie es nicht sein, weil die Nachrichtenmeldungen und der Anstieg ja das Verhalten der Leute beeinflusst), und die gezeigte Kurve das im Prinzip richtig beschreibt.
Aber von exponentiellem Wachstum zu reden und dann eine Normalverteilung zu zeigen, die ein Maximum zeigt und dann auch wieder nachlässt, passt einfach nicht, weil es eben keine Exponentialkurve mehr ist. Selbst wenn man sich auf die Spitzfindigkeit einlassen wollte, dass die Dichtefunktion der Normalverteilung sehr wohl eine Exponentialfunktion ist, ist sie durch den negativen Exponenten und die Quadrierung keine exponentielle Wachstumsfunktion. Überspitzt gesagt für mathematische Primelkacker: Auch eln(x) ist keine Exponentialfunktion, obwohl die Exponentialfunktion die Hauptfunktion darin ist. Das Ergebnis ist trotzdem linear. Nur weil eine Exponentialfunktion drin vorkommt, ist nicht immer auch das Ergebnis exponentiell.
Oder anders gesagt: Gerade in Zeiten nachlassender mathematischer Bildung halte ich es für verfehlt, von exponentiellem Wachstum zu sprechen und eine Normalverteilungskurve zu zeigen (auch wenn in deren Funktion eine Exponentialfunktion vorkommt), weil eine Exponentialfunktion eben klassisch immer durchgehend nur Steigung (oder bei negativem Exponenten immer Fallen) hat und nicht mal rauf und mal runter geht. Begründung: Kurvendiskussion. Die Ableitung der Funktion betrachten.
Ich glaube aber nicht, dass die bei der Tagesschau so weit gedacht und sich Gedanken darüber gemacht haben, ob Titel und Graphik zusammenpassen.